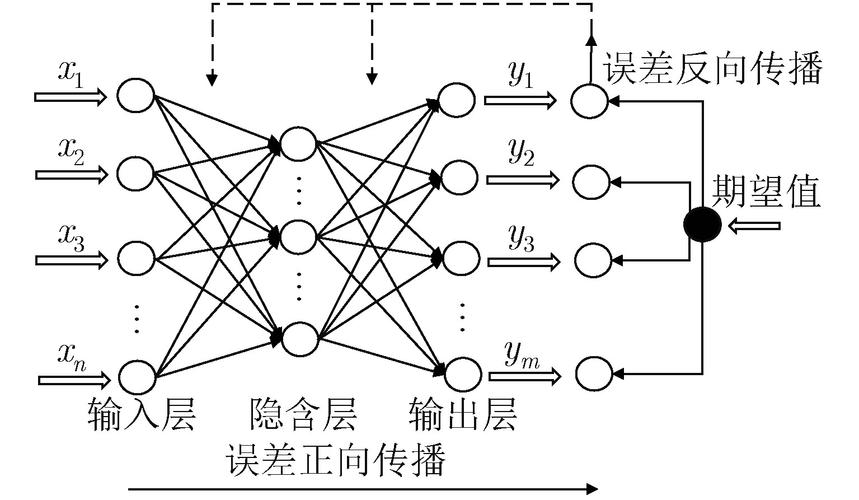
策略思维
从对方的立场思考问题,在考虑对方可能的行为基础上采取有利于自己的行动
均衡分析
预测博弈的可能结果,理解个体理性与集体理性的冲突
"要想在现代社会做一个有文化的人,你必须对博弈论有一个大致了解。"
— 保罗·萨缪尔森
1. 博弈论概述
1.1 博弈论的定义与核心思想
博弈论,英文为Game Theory,是一门研究决策主体在特定规则和条件下,如何进行策略选择以及这些选择如何导致最终结果的数学理论[5]。博弈论的核心思想在于,每个参与者的决策不仅取决于自身的偏好和可用策略,还受到其他参与者决策的显著影响。
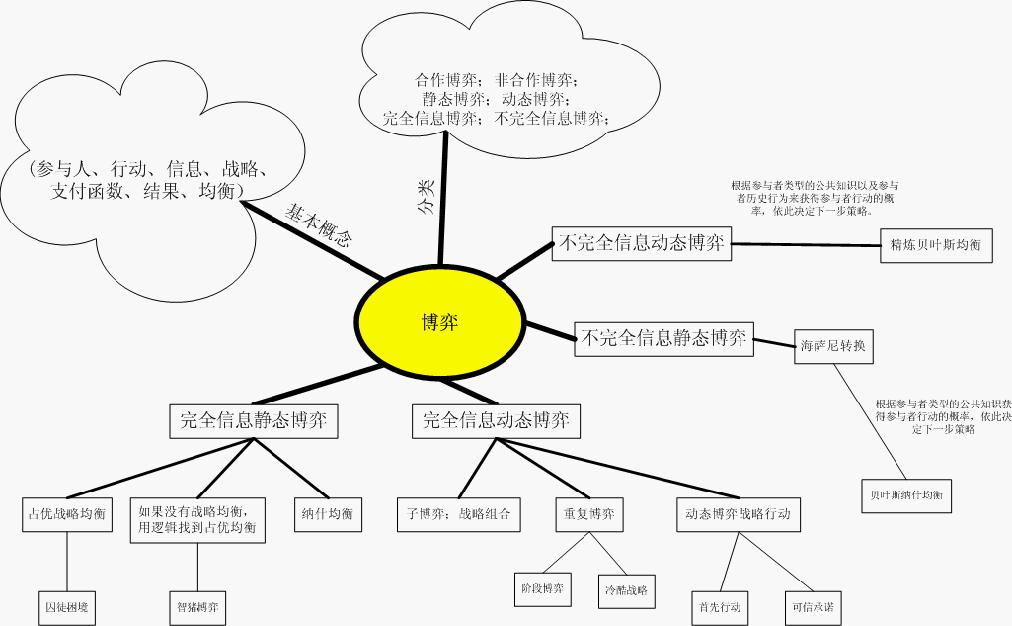
博弈论核心要素关系图
博弈论的基本要素通常包括参与者、行动(或策略)、信息、收益(或支付)和均衡 [2]。博弈论的精髓在于基于策略性相互依赖基础上的理性思考,即在选择自身行动时,不仅要考虑自身得益,还应当用他人的得益去推测他人的行动。
1.2 博弈论的历史与发展
现代博弈论的正式奠基通常被认为是20世纪上半叶。1944年,约翰·冯·诺依曼和奥斯卡·摩根斯特恩合著的《博弈论与经济行为》的出版,标志着系统化博弈理论的初步形成[328]。
随后,约翰·纳什在20世纪50年代初做出了开创性的贡献,他提出了"纳什均衡"的概念,并证明了在包含混合策略的情况下,纳什均衡在n人有限博弈中的普遍存在性[9]。
1.3 博弈论的重要性与应用价值
博弈论的重要性在于它提供了一种独特的视角和分析框架,帮助我们理解在充满不确定性和动态变化的环境中,个体或组织如何做出理性的决策。掌握博弈论的思维方法,有助于我们更好地应对并非黑白分明、二元对立的复杂世界 [1]。
经济学应用
市场结构分析、企业竞争策略、拍卖机制设计
政治学应用
选举策略、国际关系、政策制定
计算机科学
算法设计、网络协议、人工智能
2. 博弈论的核心概念
参与者 (Players)
参与者是博弈论模型中的核心要素之一,指的是在博弈过程中进行决策并承担相应后果的个体、团队或实体[2]。每个参与者都有自己的目标,即最大化自身的利益或效用。
策略 (Strategies)
策略是博弈论中另一个至关重要的概念,它指的是参与者在博弈中可供选择的完整行动方案或决策规则[2]。策略可以分为纯策略和混合策略。
收益 (Payoffs)
收益是参与者在特定策略组合下所获得的效用或回报 [3]。收益是衡量博弈结果对参与者价值的标准,它可以是金钱、资源、利润、效用值或其他任何参与者关心的度量方式。
信息 (Information)
信息在博弈论中扮演着关键角色,它指的是参与者在做出决策时所拥有的关于博弈状态、其他参与者的特征、策略空间以及收益函数等方面的知识[3]。
均衡 (Equilibrium)
均衡是博弈论中的一个核心概念,指的是一种所有参与者都不再愿意单方面改变自身策略的稳定状态[3]。纳什均衡是最著名和最重要的均衡概念。
理性 (Rationality)
理性是博弈论分析中的一个基本假设,它指的是参与者在博弈过程中会努力追求自身利益的最大化,并根据所掌握的信息进行逻辑一致的决策[125]。
3. 博弈论的基本分析方法
3.1 标准式博弈 (Normal Form Games)
标准式博弈,也称为策略式博弈或矩阵式博弈,是描述博弈的一种常用形式,特别适用于静态博弈,即所有参与者同时选择行动[2]。
常用分析方法:
- • 严格占优策略:在任何情况下都优于其他所有策略的策略
- • 严格劣策略:在任何情况下都劣于另一个策略的策略
- • 迭代剔除严格劣策略(IESDS):通过重复剔除严格劣策略来简化博弈[106]
- • 纳什均衡:寻找所有参与者都无法通过单方面改变策略来获得更高收益的策略组合
3.2 扩展式博弈 (Extensive Form Games)
扩展式博弈是描述博弈的另一种重要方式,特别适用于分析动态博弈,即参与者的行动有先后顺序,并且后行动者能够观察到先行动者的部分或全部行动[100]。
分析方法:逆向归纳法
从博弈树的末端开始分析,确定在该阶段行动的参与者的最优选择。然后,倒推到前一个阶段,将该阶段参与者的最优选择作为已知条件,分析前一阶段参与者的最优选择。通过逆向归纳法找到的策略组合称为子博弈精炼纳什均衡。
3.3 纳什均衡 (Nash Equilibrium)
纳什均衡是博弈论中一个核心且广泛应用的概念,由数学家约翰·纳什提出,用于描述非合作博弈中的一种稳定状态[9]。在一个策略组合中,如果给定其他所有参与者的策略,没有任何一个参与者可以通过单方面改变自己的策略来获得更高的收益,那么这个策略组合就构成了一个纳什均衡。
纯策略纳什均衡
所有参与者都选择确定性策略的均衡
混合策略纳什均衡
参与者以一定概率分布随机选择不同纯策略的均衡
3.4 重复博弈 (Repeated Games)
重复博弈是指同一个博弈被重复进行多次的博弈过程 [100]。重复博弈为合作行为的出现提供了可能性,即使在一次性博弈中合作不是均衡策略。
无名氏定理 (Folk Theorem)
在无限次重复博弈中,如果参与者对未来有足够的耐心,那么许多在一次性博弈中不可行的收益组合(包括合作带来的更高收益)都可以作为重复博弈的均衡结果出现。
4. 经典博弈模型与案例分析
4.1 囚徒困境 (Prisoner's Dilemma)
囚徒困境是博弈论中最著名且最具代表性的非零和博弈模型之一,它深刻地揭示了个人理性与集体理性之间的冲突[12]。
关键洞察
无论对方如何选择,坦白对自己而言都是更优的策略。结果,两个理性的囚徒都会选择坦白,这比双方都抵赖的结果要糟糕得多。
收益矩阵
| 囚徒A\囚徒B | 坦白 | 抵赖 |
|---|---|---|
| 坦白 | (-5, -5) | (0, -10) |
| 抵赖 | (-10, 0) | (-1, -1) |
纳什均衡:(坦白,坦白)
现实应用
军备竞赛
各国增加军备以确保安全,但导致集体不安全
价格战
企业降价争夺市场,导致行业利润下降
环境问题
个体过度使用公共资源,导致资源枯竭
4.2 智猪博弈 (Pigs' Game)
智猪博弈是一个经典的博弈模型,常用于分析在实力不对等的参与者之间,如何进行策略选择以及"搭便车"现象的产生[21]。
均衡结果
小猪的占优策略是等待,大猪的最佳策略是自己去踩踏板。博弈的均衡结果是:小猪等在食槽边,大猪为了一点残羹奔忙于踏板和食槽之间。

现实启示
智猪博弈揭示了在团队合作或公共品供给中,实力较弱或付出成本较高的一方可能会选择"搭便车",而实力较强或付出成本相对较低的一方则可能承担更多责任。这对企业管理和激励机制设计有重要启示。
4.3 猎鹿博弈 (Stag Hunt)
猎鹿博弈,又称信任博弈或协调博弈,强调了合作带来的巨大潜在收益以及合作所需的信任和协调[34]。
存在两个纳什均衡:合作猎鹿(高风险高收益)和各自猎兔(低风险低收益)
4.4 斗鸡博弈 (Chicken Game)
斗鸡博弈,又称鹰鸽博弈或胆小鬼博弈,是描述冲突升级和威慑策略的经典模型。
存在两个纯策略纳什均衡:一方前进,另一方后退;或者反之
5. 博弈论在不同领域的应用
6. 博弈论解决实际问题的案例详解
6.1 商业竞争中的博弈分析
博弈论为理解和分析商业竞争提供了强大的理论框架和工具,帮助企业洞察竞争对手的策略,预测市场动态,并制定有效的竞争策略。
可口可乐 vs 百事可乐:百年竞争
在可口可乐与百事可乐的百年竞争中,双方在价格、广告、产品创新等多个维度展开了激烈的博弈[69]。
价格博弈
双方都面临着是否涨价的选择。如果都不涨价,各自获得一定利润;如果一方涨价而另一方不涨,不涨价的一方将获得更大市场份额和利润;如果都涨价,则可能共同分享更高的利润。
营销策略
百事可乐通过"百事挑战"等营销活动,以及针对年轻人的品牌定位,成功挑战可口可乐的市场地位。可口可乐则通过经典的广告宣传进行反击。
博弈论启示
博弈论能够帮助企业识别竞争中的关键因素,预测对手的行为,并制定出更具前瞻性和有效性的竞争策略,从而在复杂的市场环境中获得竞争优势。
6.2 环境保护与公共资源管理
环境保护和公共资源管理是博弈论应用的重要领域,因为这些情境往往涉及到个体理性与集体理性的冲突,以及"公地悲剧"问题。
公地悲剧 (Tragedy of the Commons)
多个个体共同拥有一种公共资源,每个个体都有权使用该资源,并从使用中获益。然而,如果每个个体都追求自身利益最大化,过度使用公共资源,最终会导致资源枯竭或环境恶化。
解决思路
- • 建立明确的产权和有效的监管机制
- • 设计激励机制和惩罚措施
- • 促进参与者之间的沟通和信任

国际环境协议
各国需要就减排目标达成一致,并建立有效的监测和履约机制,以确保协议的有效性。这本质上是一个重复博弈问题。
6.3 交通管理与城市规划
博弈论在交通管理与城市规划领域有着重要的应用价值,尤其是在分析个体出行选择与整体交通系统效率之间的关系方面。
上海私车牌照拍卖制度
上海私车牌照拍卖制度是博弈论在公共政策制定中的一个应用实例 [35]。上海通过每月拍卖一定数量的私车牌照来控制机动车总量,缓解交通压力。
最初方案
出价最高的前若干名报价者获胜,并支付各自所报出的价格。导致一些参与者觉得不公平。
改进方案
采用"次高价中标"的维克瑞拍卖形式,引导更理性的投标行为,缓解对公平性的争议。
7. 博弈论的学习路径与资源推荐
7.1 入门书籍与课程
7.2 进阶学习与深入研究
8. 结论与展望
8.1 博弈论的总结与核心洞见
博弈论为我们提供了一套强大的分析工具,用以理解在复杂互动环境中理性决策者如何思考和行动。 其核心洞见在于,个体的决策并非孤立存在,而是深受其他参与者决策的影响,并反过来影响他人。
核心价值
- • 提供策略性思考的框架
- • 揭示个体理性与集体理性的冲突
- • 分析合作的可能性与条件
- • 强调信息在决策中的关键作用
应用领域
无论是在商业竞争、人际交往,还是在更广泛的社会、政治和经济问题中,博弈论都能帮助我们更清晰地分析局势,预测他人行为,并制定出更优的策略。
8.2 博弈论的未来发展趋势
博弈论作为一门不断发展的学科,其未来发展趋势将更加多元化和交叉化。与人工智能和机器学习的深度融合将是重要方向之一。
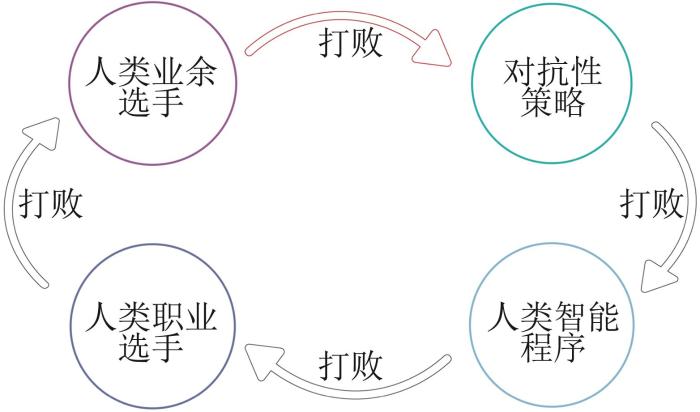
新兴应用领域
- • 气候变化与国际谈判
- • 公共卫生与疫苗接种
- • 网络安全与攻防博弈
- • 金融监管与风险控制
"随着计算能力的提升和研究方法的创新,博弈论的理论体系将不断完善,其应用边界也将持续拓展,为解决现实世界中日益复杂的策略互动问题提供更强大的支持。"